Day 99：单纯形算法

18年12月3日 · 北京理工大学-胡依梦 5638 人阅读

单纯形算法

线性规划是数学的一个领域，它处理约束优化问题的最简单形式-线性规划。

我们先来看一个标准形式的线性规划的例子。

我们的目标是将给定的一组线性约束的线性函数最大化。

单纯形算法相当简单。我们将不等式系统转化为等式系统，然后利用具有巧妙的枢轴选择的高斯消去。

如果你对我的解释感到迷糊，那么就用笔和纸，把表格改写成方程组。我们需要做的只是解线性方程组。

我们务必要注意，上述线性规划中的每个不等式都是f(X)≤b的形式。我们可以在左边加上一些非负数，得到f(X)+s=b。变量s称为松弛变量，它将补偿f(X)和b之间的差异，从而消除不等式。

通过在每个不等式中引入松弛变量，我重写了原来的问题。我还附加了要最大化的函数，并将其设置为0。为什么?

注意，方程系统有一个平凡的解。我们可以设置x=y=z=0，让松弛变量去补偿这个系统。这不是最好的解决方案，但是是一个很好的开始。

从现在开始，我们要将系统重写为Excel并使用这个表。

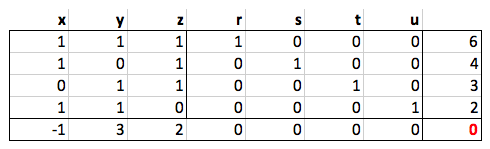此表叫单纯形表。

此处有个规则需要记住。如果有一列具有全零且这样的列只有一个，则该变量将接受非零值。否则，将此变量设置为零。

因此，初始解是x=y=z=0，r=6，s=4，t=3，u=2。这可不是巧合。要知道，我们为初学者选择了一个简单的解决方案来遵守上面的规则。而这表明了这几乎是我们解决问题所需要的一切。

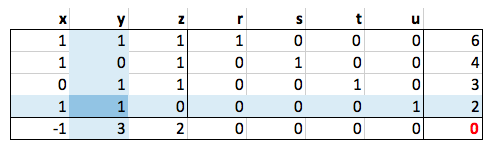最后一行包含要最大化的函数。我们不能增加x，因为函数会减少。但我们可以增加y，因为它的系数是正的。

y能增加多少呢？将最后一列[等式的右侧]除以y-列：6/1、4/0、3/1、2/1，并取y-列包含一个正数且除法结果最小的行。

我们需要取最小的值，这样我们就不会违反其他行的条件-我们仍然在解一个方程组，思考一下。

然后做高斯消去。

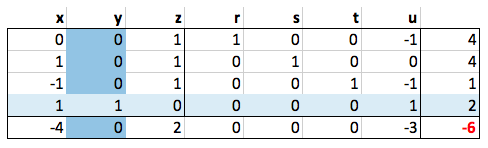注意一下这个方程组是如何变化的。还记得前面的那个规则吗？变量的值变化为x=z=u=0，y=2，r=4，s=4，t=1，函数值为6。

还有另外一个可以增加的变量。那就是z，因为它的正系数在最后一行。现在，找到正确的行并消除它。

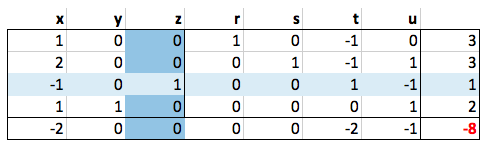现在我们可以看到最后一行不包含正值，这说明我们已经完成了。那么最终的解决办法是什么呢？

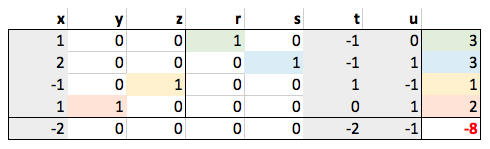设x=0，y=2，z=1，函数值为-x+3y+2z=8

我强烈建议你用纸笔写一下，下面是一些可以从方程组的角度来思考的问题，也可以有利于你理解单纯形算法。

这就是关于单纯形的全部解释了，是不是很简单呢？

一般来说，解决一个线性问题是非常困难的，理论界将单纯形转化为指数算法。

进一步来说：解可以是无界的，系统也可能退化，单纯形可能永远循环等等。但我的算法并不在乎这些，只要它能够返回至少一个解决方案。

事实上，在实践中，这是很容易的。单纯形可以 (而且通常是) 针对给定的问题具体实现，而实际问题往往能够快速有效地得到解决。

如果你对线性规划感兴趣，那么继续读更多关于这个话题的文章吧。记住，你只是在处理方程，你不会惊讶于对可行区域、对偶问题和所有理论背后的深入解释。

Python3Turtle