Day 98:龙贝格积分算法

18年12月3日 · 北京理工大学-胡依梦 7912 人阅读
龙贝格积分算法
龙贝格积分算法将扩展梯形规则和理查森外推两种公式结合起来,以便用较少的步骤得到较好的近似值。
接下来让我们以轻松愉快的方式解释它是如何工作的。
在区间(a,b)上求函数 f 的定积分的最简单的方法是使用梯形规则。
 |
在最左边的图表里你可以看到公式只是一个梯形的区域。
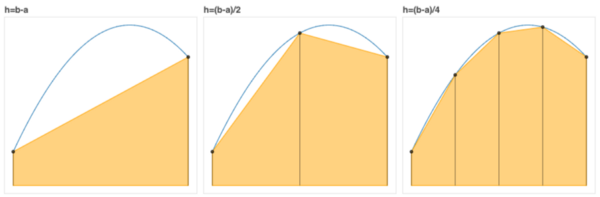 |
definite integral estimates
你还可以注意到,有一个可以使用扩展梯形规则改进的特定的错误。将间隔(a,b)分成两半,在每一半上应用梯形规则,并将它们加起来。
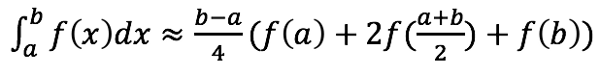 |
看中间的图案,这个公式仅仅显示出两个梯形的面积。
而看第三个图案,它包含了另外一半甚至是更好的期望值。我们可以继续这么做,直到我们对误差值感到满意。
问题就是,这种收敛速度太慢了!在此,我们可以看看理查森的援救推断。
在理查森外推中,我们将两个不好的估计值合并成一个好的估计值。而这条迪尔伯特的长条形中的描述里,你会得到最好的解释。不信你瞧。
 |
事实上,不同于迪尔伯特,我们幸运地知道每个估计值的误差界限。
换句话说,如果我们确信一种估计比另一种更好(例如,在扩展梯形规则中发现更小的间隔),我们也能知道应该向哪个方向可以得到期望的精确解。
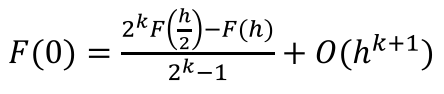 |
最后,龙贝格法建立了一个具有令人惊讶的精确结果的估计表。
 |
Romberg integration
第一列包含扩展梯形规则的结果,每一行使用的拆分是前一行的两倍。所有其他的值都是理查森外推的结果。
对角线包含了最终的估计值,每个对角线元素给出大约两位数的精度。因此,第5行和第5列的元素给出了大约10位数精度的估计值。
算法实现
e^(-x 2)的积分[0,1]
ln(2)
x的积分[0,1]
自然对数
正态分布
Python3Turtle
