Day 81：拓扑排序

1、什么是拓扑排序？

        对有向无环图（Directed Acyclic Graph, DAG）的所有顶点按照优先（必要）顺序排成一个线性序列的过程称之为拓扑排序。

        拓扑排序的结果，表现为对每一条有向边(u —> v)，均有u（在排序顺序性中）比v先出现，也可理解为对某顶点v而言，只有当v的所有源点（前置条件）均出现了，v才能出现。

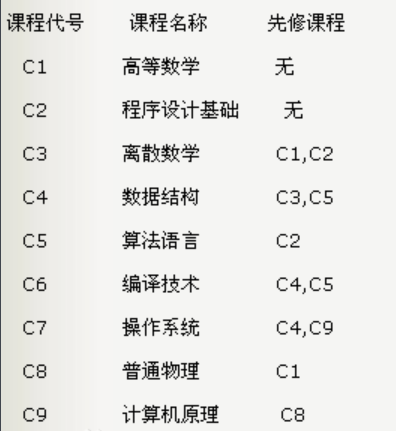                                                                                     图1

        如图1所示，通过拓扑排序可获得一个课程学习的优先级顺序列表。值得注意的是，拓扑排序的路径可能有多种，不一定是唯一的。

2、拓扑排序的用处

        拓扑排序常常被用来表示事件之间的驱动依赖关系，管理任务之间的调度。比如在并行计算中，一个程序可以被表示为DAG。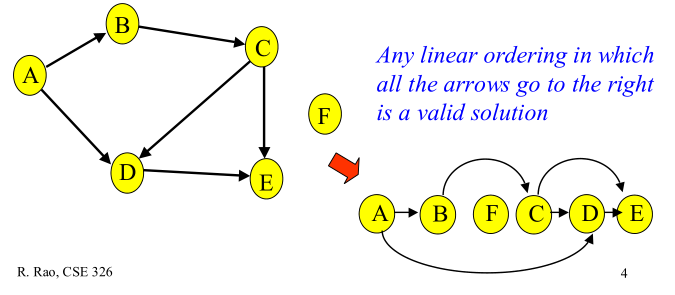

                                                                                  图2

3、“入度为零”算法解析

        如图2所示：

        A顶点有0个入度，2个出度；

        B顶点有1个入度，1个出度；

        F顶点有0个入度，0个出度；

        E顶点有2个入度，0个出度。

        很明显，拓扑序列起始顶点的入度应该为0。

        第一步：获取所有顶点的原始入度，找到入度为0的所有顶点，存入列表L0。

        第二步：取出L0中的一个顶点作为开始顶点，然后将以该顶点为前置条件的顶点的出度-1（图2中，如取出A顶点，则B、D顶点的入度-1，相当于A已经实现了，B、D的前置条件少了一个），然后判断刚刚执行“入度-1”操作的顶点（如B、D顶点）现在的入度是否为零，如果为零，则将该顶点存入L0。

        第三步：重复执行第二步，直至L0列表为空为止，输出先后从L0中取出的入度为零的顶点的顺序序列。

        第四步：判断输出序列的长度是否等于所有初始顶点的个数，如果相等，即为一个拓扑排序序列（注意：可能非唯一，获得结果可能只是其中一个可行的序列），如果小于所有顶点的个数，说明原图为有环图，也就不存在拓扑排序了。