Day 69：RMSProp（Root Mean Square Prop）

今天来聊聊机器学习的话题怎么样？RMSProp是一个基于梯度的优化方法，由Geoffrey Hinton在他的Coursera神经网络课程上提出。

神经网络的概念已经存在几十年了，但是研究者们一直没能训练出哪怕稍微复杂一点的神经网络。导致这个情况的原因有很多，比如梯度幅值就是一个很棘手的问题。

对于很复杂的函数——比如神经网络而言，在训练的过程中其梯度总会要么趋向于消失要么趋向于爆炸。而且这个效应会不断积累——函数越复杂，问题就越严重。

Rmsprop是一个非常聪明的解决办法。它采用梯度的平方的移动平均数来使梯度数得以规范。它会让步数趋于平衡——降低高梯度的步数以避免其爆炸，增加小梯度的步数以避免其消失。

我编写了三种的基于梯度的方法：

1. 梯度下降（Gradient Descent）（简单）

2. RMSProp

3. RMSProp结合 Momentum（Momentum也是一种独立的方法）

我要用分别用这三种方法去求解矩阵A的逆矩阵。损失函数（loss function）是AX和单位矩阵I之间的平方差，以及相应导数。

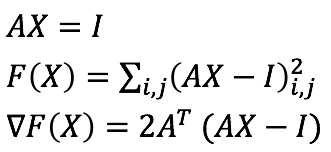下图是三种方法各自的损失函数的分布图象

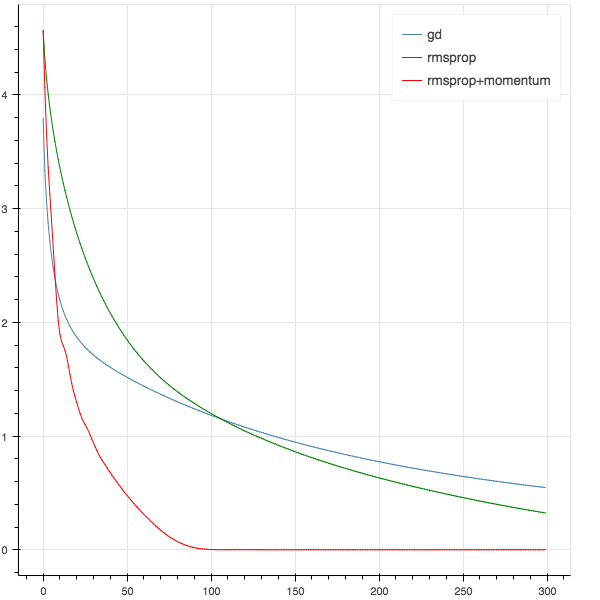我必须得说一句，这个例子并不具有代表性。RMSProp开发出来是用于小批量（mini-batch）学习的随机方法，虽说是小批量但至少是正儿八经的机器学习，本文中这种小打小闹的测试还不够显现出RMSProp的优秀表现。

算法实现

函数

优化

访问我的Github笔记本以获取完整的代码，附有结果和分布情况。